
En el complejo universo de las matemáticas, existen ciertos conceptos que capturan la imaginación tanto de académicos como de entusiastas.
Uno de estos conceptos es “e elevado a infinito”, una expresión que desafía la comprensión intuitiva y revela la profundidad y belleza inherentes al estudio matemático.
Este término no solo representa una pregunta matemática, sino que también es un punto de encuentro entre la teoría pura y las aplicaciones prácticas en campos tan diversos como la economía, la física y la biología.
Explorar el significado de “e elevado a infinito” nos lleva a un viaje a través de los principios fundamentales del cálculo y el análisis matemático. ¡Comencemos!
En el texto
✦ ¿Cuánto es e elevado a infinito?
El límite de la constante matemática e (aproximadamente 2.71828) elevado a infinito es infinito.
Esto se debe a que cualquier número mayor que uno, al ser elevado a un exponente que crece indefinidamente, tiende a aumentar sin límite.
Matemáticamente, se expresa como:
![]()
Este concepto es fundamental en áreas como el cálculo y el análisis de crecimiento exponencial en diversos campos científicos y financieros.
✦ La constante e
La constante e, conocida también como número de Euler, es uno de los números más importantes en matemáticas, junto con el 0, 1, π e i (la unidad imaginaria).
Su valor aproximado es 2.71828, y se caracteriza por ser el límite de la expresión
Esta constante es la base del logaritmo natural y juega un papel crucial en el cálculo, especialmente en el crecimiento exponencial y en los problemas de tasa de cambio.
✦ ¿Qué significa elevar a infinito?
Para explicar mejor la implicación de e elevado a infinito, es fundamental entender qué significa elevar un número a infinito.
En matemáticas, el concepto de infinito (∞) no es un número en el sentido convencional, sino una idea que representa algo que no tiene límite o fin.
Al hablar de elevar un número a infinito, nos referimos a un proceso límite; es decir, qué ocurre con una expresión a medida que el exponente crece sin límites.
✦ El comportamiento de e elevado a Infinito
⌦ Teorema fundamental
Cuando elevamos la constante e a infinito, estamos interesados en el límite de la expresión en cuando n tiende a infinito. Matemáticamente, este límite se expresa como:
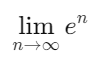
⌦ Análisis del límite
Para entender este límite, es esencial recordar que e es mayor que 1. Cuando un número mayor que 1 se eleva a un exponente que crece de manera ilimitada, el resultado tiende a crecer de forma ilimitada.
Por lo tanto, el límite de en cuando n tiende a infinito es, de hecho, infinito. En términos matemáticos, esto se puede escribir como:
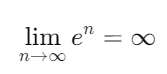
Este resultado tiene implicaciones profundas, especialmente en campos como la física, la economía y, por supuesto, la matemática avanzada, donde el crecimiento exponencial se encuentra con frecuencia.
✦ Implicaciones y aplicaciones
⌦ Crecimiento exponencial
En el mundo real, el concepto de e elevado a infinito se manifiesta en fenómenos de crecimiento exponencial.
Por ejemplo, en biología, la población de una especie en condiciones ideales puede crecer de manera exponencial, siguiendo una curva que se asemeja a en.
⌦ Cálculo de Intereses compuestos
En finanzas, la fórmula del interés compuesto continuo utiliza la base e. La idea de “interés sobre interés” a lo largo del tiempo puede conceptualizarse como elevar e a una tasa de interés multiplicada por el tiempo, acercándose a infinito en teoría bajo un plazo ilimitado.
⌦ Física y leyes naturales
En física, ciertas leyes y constantes involucran la constante e, especialmente en la mecánica cuántica y en la teoría de la relatividad de Einstein. Aquí, el concepto de infinito y su relación con e adquiere un significado práctico y teórico.
⌦ Conclusión
El análisis de e elevado a infinito nos lleva a una comprensión más profunda de conceptos fundamentales en matemáticas y su aplicación en el mundo real.
Esta exploración no solo es un ejercicio de comprensión teórica, sino que también abre puertas a la aplicación práctica en ciencia, ingeniería y finanzas.
Así, aunque puede parecer un concepto abstracto, tiene implicaciones reales y profundas en nuestra comprensión del universo y en la aplicación de la ciencia y la tecnología en nuestra vida diaria.